几何画板如何制作三维波纹？

数学中的坐标系有平面的，也有三维的，在平面坐标系上可以画出图像，那么在三维坐标系上，也是可以实现的。前面的教程中给大家介绍了用几何画板三维坐标制作的马鞍面，之后有版友提出如何画三维波纹？为了方便大家学习，在此小编整理了一个我们版友自学制作三维波纹的教程，供大家学习。

几何画板制作的三维波纹示例：

在几何画板中构造的三维波纹示例

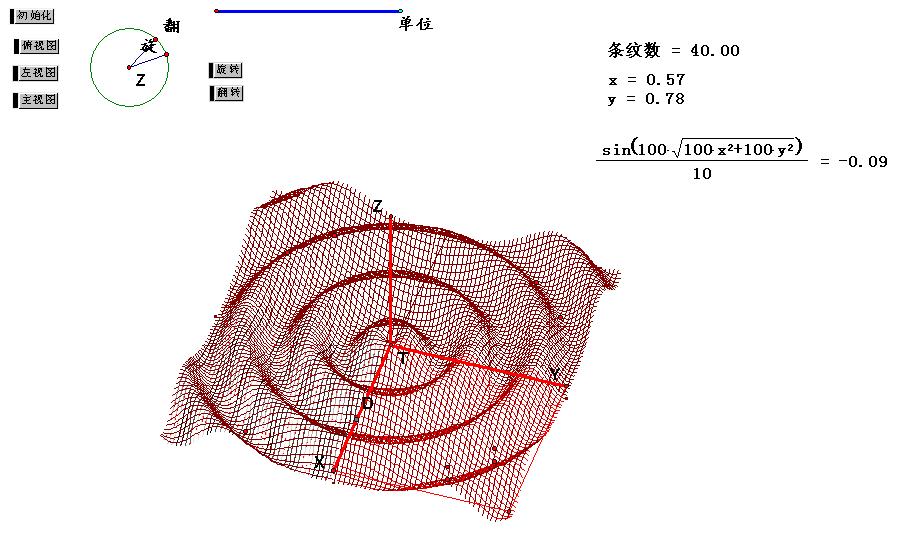
具体的制作方法如下：

步骤一 在建好三维坐标系之后，首先制作工具：平面网格，效果如下图所示。

在几何画板制作平面网格示例

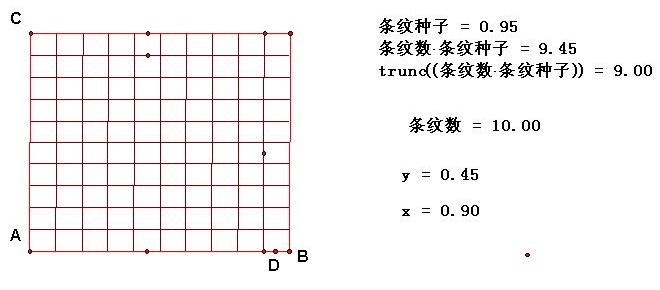
制作方法如下：

给出一个独立参数，取名横向条纹，代表线段的条数。

给出两条有公共定点线段（作为一个自己定义的坐标系），调节到近似的垂直状态。

作两条公共定点线段作为定义的坐标系示例

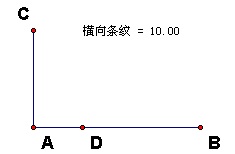
计算出AD和AB的长度的比，于是就得到一个从0到1变化的量，用这个量来作为来描述那些线段的基础，称为条纹种子。

步骤二 用如下图所示的公式计算出两个量

用公式进行计算示例

可以看得出来，最后的一个数据给出了几个离散的量，恰好是几个等分点。就是把0到1分成横向条纹数等份，这些就是分点。又可以看到倒数第2个量，是一个小数函数，那么就重复的从0到1连续变化，那么，我们把这两个量作为坐标描在自己定义的坐标系内（平行线的交点的方法）这样，这个点关于D点的轨迹就是上面的线段。

同样我们可以把纵向的画出来，当然，我们如果想要让很横向与纵向的条数一样的话，就颠倒过来，描出轨迹就可以了，这里就按照后一种方法处理。

步骤三 将网格工具与三维坐标系的XOY平面和并（通过合并端点到直线上的点的方式），就得到如下图所示的效果。

通过合并得到的三维网格示例

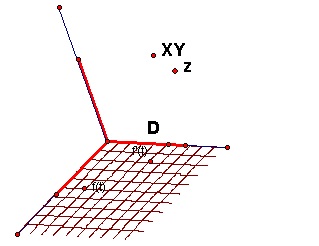
图中的动点的坐标就是（x，y），再将此动点按z轴方向平移，将平移后的点按下列计算值（其中的倍数可以自行调节，以改变单位空间中波浪的个数）进行缩放，从而得到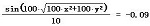 曲面上的动点，将此动点按网格上的D点求轨迹，即可得到第一象限上的图像，然后借助对称变换，作出其他象限上的图像。

以上就是我们几何画板版友制作三维波纹的思路，你看了以上步骤，对制作三维波纹有一定了解了吗？如果还是茫然，建议大家按照以上思路多练习几遍，肯定会掌握的。马鞍面也是建立在三维坐标系上面的，具体课件可参考：利用几何画板动态演示马鞍面。