几何画板演示无河宽最短距离

几何画板是绘制几何图形的一个好工具，在分析很多的实际生活问题时，采用作图的方法可以将问题解释得更清楚，这个作图过程就可以用几何画板来演示。以无河宽的过河最短距离为例，下面来介绍几何画板演示最短距离的分析过程。

几何画板演示无河宽过河最短距离课件样图：

几何画板演示《无河宽过河最短距离》课件示例

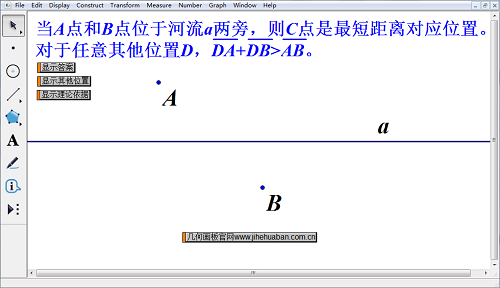
在这个课件中，A、B两点分别居于河的两侧，从A过到B点寻求最短距离的过河点，此时不考虑河宽。这也是一个很经典的问题，在学习几何的过程中经常会遇到。

点击课件中的“显示答案”就可以显示出正确的作图了，在这个作图中，直接将A、B两点以线段连接起来，与表示河流的直线a的交点就是最短距离的过河点。而想要证明这一点是最短距离的点，在直线a上任意取一点进行分析，这个过程直接点击“显示其它位置”这个上按钮就可以显示出来，课件中显示了除C点以外的任意一点D，将AD、BD连接起来形成一条折线段。而要证明线段AB点是最短的，即交点C为是佳位置点，只要了解“两点之间线段最短”这个理论就可以了，此时点击“显示理论依据”就可以看到了。

另外，要理解AB是最短距离，也可以在三角形ABD中来进行，两边之和大于第三边，所以|AB|<|AD|+|BD|，因此AB是最短的，而AB与直线a的交点C就是短距离的位置点。

点击下面的“下载模板”就可以将课件下载下来进行演示了，几何画板演示最短距离的问题，可以让学生很清楚地看到这个分析的过程，省去了直接在课堂进行作图的过程，课堂效率会更高。几何画板绘制几何作图都可以这样来进行演示，让学生一眼就看到这样的作图过程，并且清晰明了，理解时不会有其它因素进行干扰，如果想要了解更多几何画板作图演示的课件，可以参考教程：几何画板演示过河最短距离。