利用几何画板制作雪花曲线课件

“雪花曲线”一般指科克曲线，是平面图形，它的定义是：设想一个边长为1的等边三角形，取每边中间的三分之一，接上去一个形状完全相似的但边长为其三分之一的三角形，结果是一个六角形。现在取六角形的每个边做同样的变换，即在中间三分之一接上更小的三角形，以此重复，直至无穷。外界的变得原来越细微曲折，形状接近理想化的雪花。为了演示这一制作过程，可以借助几何画板来实现，下面学习具体的制作技巧。

几何画板制作的雪花曲线样图：

几何画板课件模板——制作的雪花曲线示例

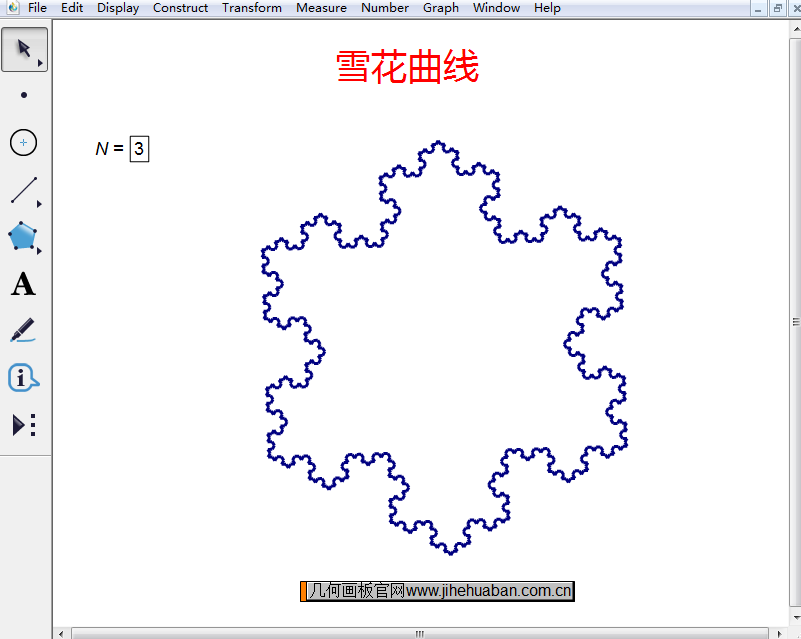
它的面积是有限的而周长却是无限的，它是从一个等边三角形开始，一步一步作出来的。

第一步：把等边三角形的各边三等分，从每条边三等分后的中段，向外作小等边三角形，再去掉与原来等边三角形重叠的边。

为了便于叙述，以后把这个过程简称为“变化”。

第二步：对上一步得到的小等边三角形，重复上面的变化。

第三步：再对上一步得到的小等边三角形，重复上面的变化。

第四步：再对上一步得到的小等边三角形，重复上面的变化。

第五步、第六步……照这样一直进行下去，就得到“雪花曲线”。

“雪花曲线”是一个边长、边数不断变化，同一图形边长相等的对称图形。所以，必须首先研究一下图形的边数、边长和面积的变化规律。

观察发现：

规律一：每次变化后，原来等边三角形的一条边，所形成的折线包括4条线段，所以，新图形的边数是原图形的4倍，而边长是原图形的1/3；

规律二：每次变化后，原来等边三角形的一条边上，所作的小等边三角形的面积，是原来等边三角形面积的1/9。

因为，周长＝边长×边数，而每次变化后，边长是原来的1/3，边数是原来的4倍，所以，周长是原来的1/3×4＝4/3。也就是说，每次变化后，边长都比原来增加1/3。随着变化的持续进行，周长会变得越来越大，以至无穷。

这就是“雪花曲线”的非同寻常之处：它的面积是有限的；它的周长却是无限的。

点击下面的“下载模板”按钮，即可下载该课件，用来演示制作的雪花曲线。该曲线是一个无限构造的有限表达，每次变化面积都会增加，但是总面积是有限的，不会超过初始三角形的外接圆。利用几何画板迭代功能可以制作雪花曲线，具体教程可参考：如何用几何画板绘制雪花图案。