几何画板演示函数的奇偶性

几何画板不只在绘制几何图形时使用很强大，同样的，它在函数图象地绘制方面也能发挥强大的功能，在用几何画板绘制函数图象时，同样也能演示出函数的奇偶性。下面就来介绍几何画板函数函数奇偶性的过程。

几何画板演示函数的奇偶性课件样图：

几何画板演示《函数的奇偶性》课件示例

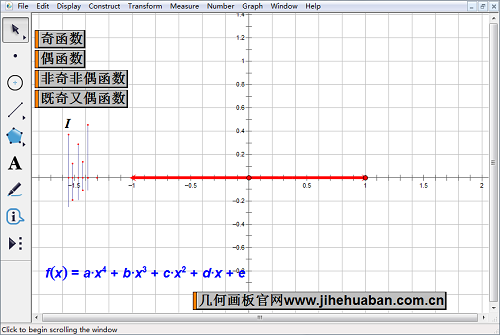
在这个课件中，点击“奇函数”按钮，图象就会变成一奇函数的图象，从图中也可以看到这具图象是呈中心对称的。点击“偶函数”按钮时，图象会变成一个偶函数的图象，我们最熟悉最常见的偶函数就是对称轴为x=0的二次函数，“点击非奇非偶函数”按钮时，图象就会变成另外一个图象，这个图象不具有对称性，而点击“既奇又偶函数”按钮时就会再次出现相应的函数图象，而这种图象兼具有奇函数与偶函数的性质与特点。

奇函数的定义：如果对于一个定义域关于0对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数。图象关于原点对称。

偶函数的定义：如果对于函数f(x)的定义域内任意的一个x，都有f（x）=f（-x），那么函数f（x）就叫做偶函数。图象关于y轴对称。

函数的奇偶性是一个很重要的性质，利用这个性质可以省去很不必要的计算过程。利用这个性质，也可以解决很多看似很复杂的问题。

点击下面的“下载模板”就可以下载课件进行演示了。几何画板函数奇偶性的演示，再配合老师的讲解与分析，学生就能够理解函数奇偶性的概念了。当然函数的奇偶性还有一些特别的性质，但是这些需要老师的深入解析，不是仅仅靠演示就可以得出的。几何画板函数性质的演示能够让学生加深对函数的学习与理解。如果想要了解更多几何画板绘制函数课件，可以参考教程：几何画板演示函数单调性。