如何用几何画板构造梯形内角平分线

在利用几何画板画图时，常常会需要做出一些符合条件要求的图形，从已知条件来作出最终的几何图形。下面介绍利用几何画板构造梯形内角平分线的方法。

例如：梯形ABCD中，AD∥BC，AB=AD+BC，E是CD的中点。求证：AE、BE分别平分角BAD、角ABC。

1.利用线段工具中的射线工具按下Shift键作出梯形两底所在的射线，利用线段工作作出梯形的腰AB。

利用射线工具和线段工具构造梯形的两底和腰AB

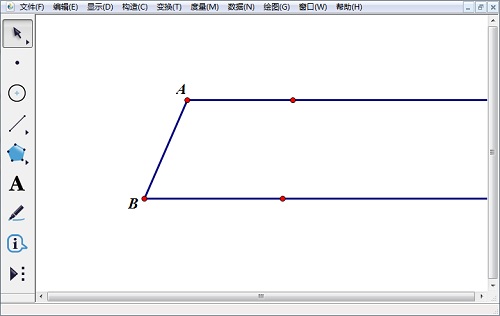
2.利用点工具在线段AB上任取一点F，选中点A和点B，选择“构造”——“以圆心和圆周上的点绘圆”，相同的方法构造圆B，两圆与两底所在的射线交于点D、C，显然，AD+BC=AB。

分别利用点A、B为圆心构造两个圆与两底的交点为D、C

3.选中点C、D，选择“构造”——“线段”构造出线段CD，选中线段CD，选择“构造”——“中点”构造出线段CD的中点E，利用线段工具构造线段AE、BE。

构造线段CD与线段的中点E并构造梯形的角平分线

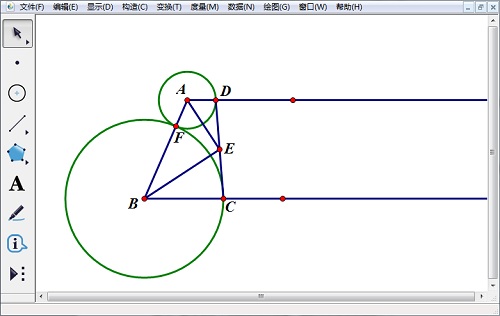
4.选中点A、D，选择“构造”——“线段”构造出线段AD，同样的方法构造线段BC，将圆A、圆B和点F和两条线段隐藏，得到符合条件的图形。

将圆A、圆B和点F和两条线段隐藏

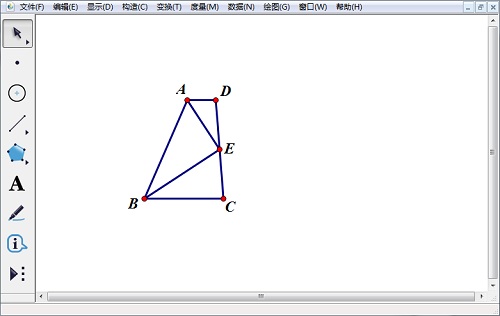
以上内容向大家介绍了按照已知条件用几何画板构造梯形内角平分线的过程。操作过程还是很简单的，易于大家的理解。几何画板角平分线是很容易构造的，在运用时需要考虑其是否可以直接使用。如果需要了解更多有关几何画板四边形的作法，可以参考教程三角形割补成平行四边形的方法。