用几何画板验证三角形重心坐标公式

在学习三角形的重心知识的时候，必要提到的就是三角形的重心坐标公式，以前老师都是利用逻辑推理的方法为学生讲解的，现在有了几何画板这个辅助教学工具，利用它可以轻松验证这个结论，从而加深学生对这个公式的理解应用。下面我们就一起来学学利用几何画板验证三角形重心坐标公式的方法。

具体的操作步骤如下：

步骤一 打开几何画板，执行“绘图”——“定义坐标系”命令，新建平面直角坐标系，并将原点坐标的标签改为O。执行“绘图”——“隐藏网格”命令，将坐标系中的网格隐藏。

在几何画板中建立坐标系示例

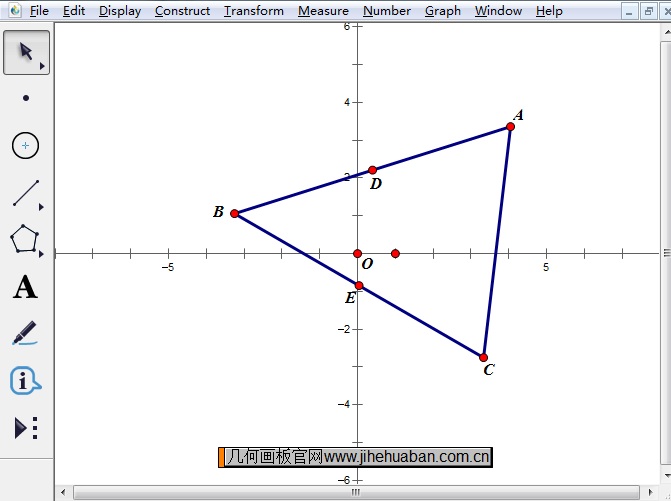
步骤二 单击左侧工具栏“多边形工具”，在画板上绘制三角形ABC，同时选中线段AB和线段BC，执行“构造”——“中点”命令，作出两条线段的重点D、E。

绘制三角形ABC示例

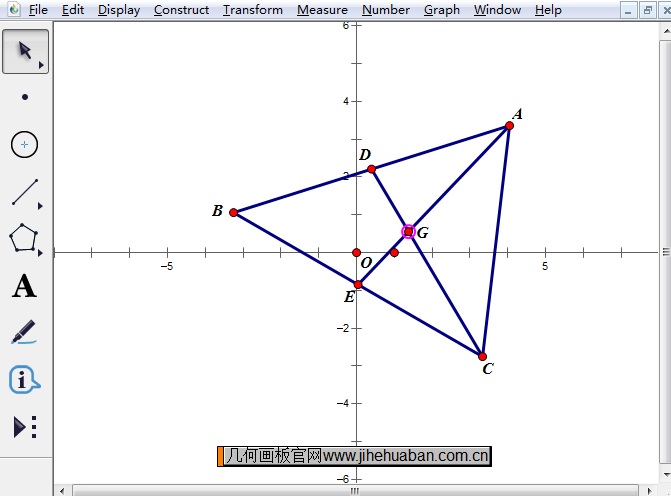
步骤三 同时选中点A和点E，执行“构造”——“线段”命令，构造三角形的中线AE。同样地，构造中线CD。同时选中点线AE和线段CD，执行“构造”——“交点”命令，构造三角形ABC的重心G，如下图所示。

绘制三角形ABC的重心示例

步骤四 同时选中点A、B、C，执行“度量”——“横坐标”命令，度量出它们的横坐标。按同样地方法，度量出点A、B、C的纵坐标和点G的坐标，完成后如下图所示。

利用度量菜单度量点的坐标示例

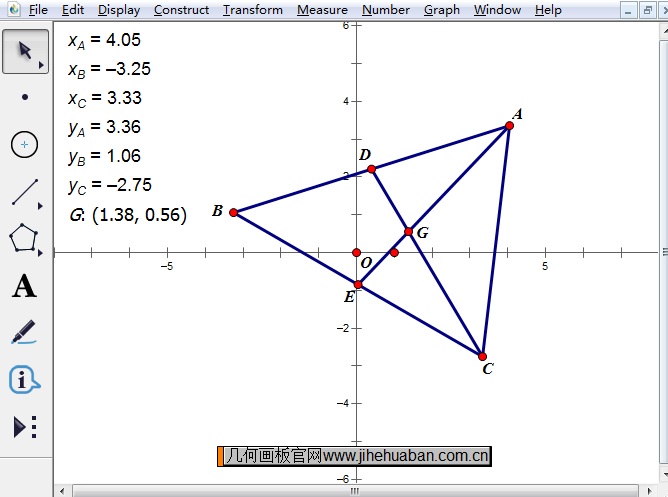
步骤五 执行“数据”——“计算”命令，在弹出的“新建计算”对话框中计算出（X_A+X_BCA+ Y _BC

利用计算命令计算三点的坐标平均数示例

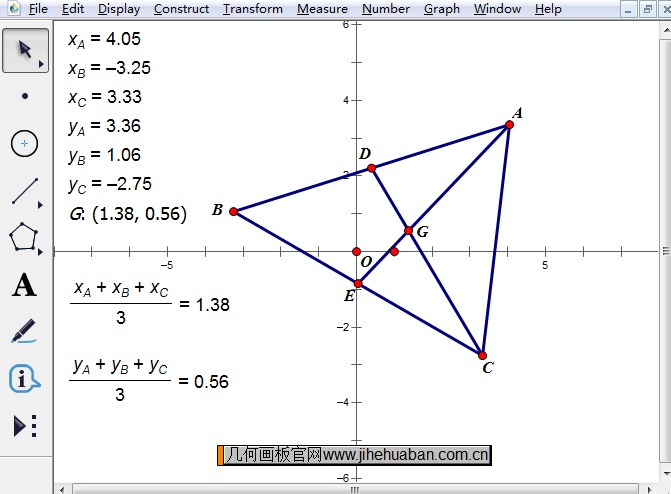
步骤六 此时拖动三角形的三个顶点可以改变三角形的形状，同时可以观察重心的坐标变化，由此验证了在平面直角坐标系中，重心的坐标是顶点坐标的算术平均数。

改变三角形形状验证三角形重心坐标公式

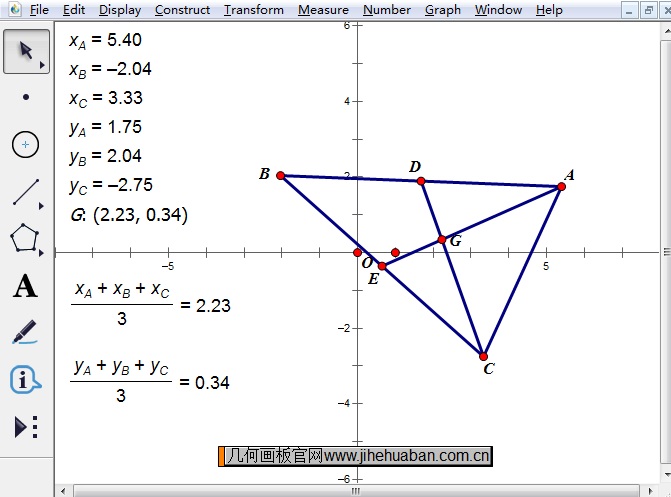
以上给大家详细介绍了用几何画板验证三角形重心坐标公式的方法，由此可见，在教学中，运用动态几何软件几何画板进行研究性学习是很有必要的，让学生通过作图、拖动图来观察几何图形，从而发现几何图形的特征及相互关系，并作出猜想和验证。在前面的教程中，还讲解了用几何画板验证海伦公式的方法，具体教程可参考：利用几何画板验证海伦公式。