用几何画板验证三角形重心定理

重心原是一个物理概念，对于等厚度的质量均匀的三角形薄片，其重心恰为此三角形三条中线的交点，重心因而得名。几何画板作为学习几何的辅助工具，可以用来验证三角形中的几何定理，下面就一起来看看如何用几何画板验证三角形重心定理。

几何画板制作的验证三角形重心定理课件样图：

几何画板课件模板——验证三角形重心定理示例

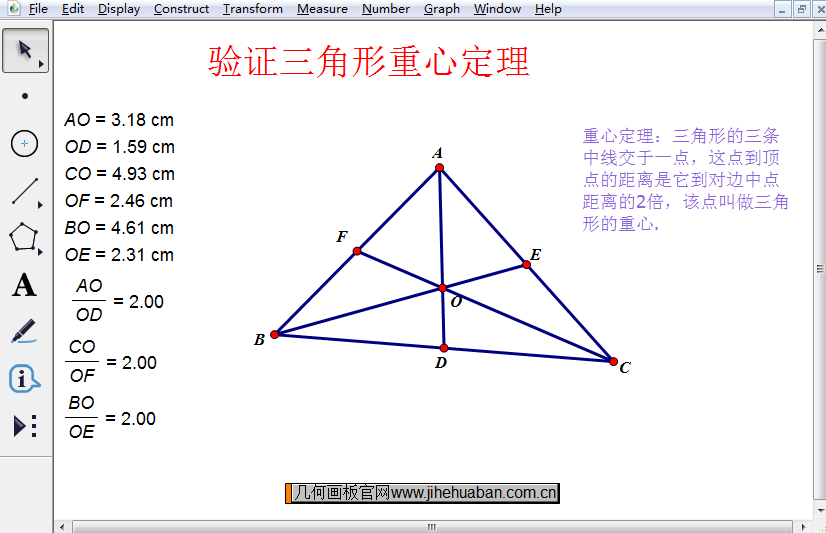
在该课件中，首先分别度量了三角形中以重心点O为界限的线段AO、OD、CO、OF、BO、OE的距离，然后通过利用“数据”——“计算”命令计算出了AO/OD、 CO/OF、BO/OE的值，发现重心到三角形顶点的距离是重心到对边中点距离的2倍。另外，我们还可以使用“移动箭头工具”任意拖动三角形ABC的任意顶点，改变三角形的形状，发现不管三角形的重心怎么变化，其重心到三角形顶点的距离永远是重心到对边中点距离的2倍，这样就验证了重心定理的正确性。

通过学习该课件，还可以延伸以下重心的性质：

1.重心和三角形3个顶点组成的3个三角形面积相等。即重心到三条边的距离与三条边的长成反比。

2.重心到三角形3个顶点距离的平方和最小。

3.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其重心坐标为（（X₁+X₂+X₃）/3，（Y₁+Y₂+Y₃）/3）。

点击下面的“下载模板”按钮，即可下载该课件，用在三角形重心定理一课的讲解中，用来验证该定理的恒成立。三角形中还包括了中位线定理，在前面的教程中有介绍用几何花瓣验证三角形中位线定理的方法，具体大家可参考：用几何画板验证三角形中位线定理。