几何画板演示直线绕定点旋转的动画

利用几何画板可以将静态的抽象过程转化为动态的象形化，在这个将抽象化为具体的过程中，使得一些不易于理解的问题以一种具体的形象展现人们眼前。人们总是对能够用眼睛看到东西容易理解，在几何图形的变换过程中这一点也不例外。在对于函数的研究中，我们也经常对函数进行变换研究，下面就来介绍几何画板演示直线绕定点旋转的动画过程。

几何画板演示直线绕定点旋转的动画课件样图：

几何画板演示《直线绕定点旋转的动画》课件示例

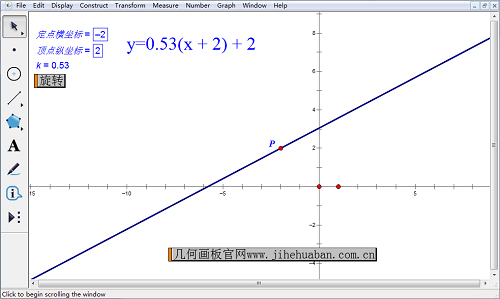
在这个课件中，利用几何画板作出了一个一次函数的图象，一次函数是一条直线。图象要绕定点进行旋转，这个定点是（2，-2），点击课件中的“旋转”按钮时，函数图象就会绕这个上点进行旋转。在旋转的过程中，我们可以看到函数表达式在不停地发生变化，与之相应的就是斜率k的变化。一次函数图象的倾斜程度直接由斜率k决定，因此当直线不停地旋转时，它的倾斜触角度是在不断变化的，表现在表达式上就是斜率的变化。当然斜率在发生变化时，截距也是在发生变化的，这可以从表达式的常数项中观察到。

一次函数的图象比较简单，在理解时也比较好理解，而对于图象地变换也是很直观的，当用几何画板演示出这个过程时，就会很简单，也很容易计算。这是学习二次函数变换的基础。

以上内容向大家介绍了几何画板直线绕定点旋转的动画课件。几何画板演示函数变换的过程可以将抽象地代数转化为具体地图形，将图形与计算结合才会更加容易对问题进行分析。如果想要了解更多几何画板函数动画课件，可以参考课件：几何画板演示反比例函数图象的变换。