利用几何画板探讨椭圆的离心率

在学习椭圆这个圆锥曲线时，会接触到离心率这个概念，它是椭圆扁平程度的一种量度，离心率定义为椭圆两焦点间的距离和长轴长度的比值，用e表示。也可以形象地理解为，在椭圆的长轴不变的前提下，两个焦点离开中心的程度。为了让学生们容易理解离心率对椭圆形状的影响，可以利用几何画板作图，来演示离心率对椭圆形状的影响，下面就一起来学习具体制作技巧。

几何画板制作的探讨椭圆的离心率课件样图：

几何画板课件模板——探讨椭圆的离心率示例

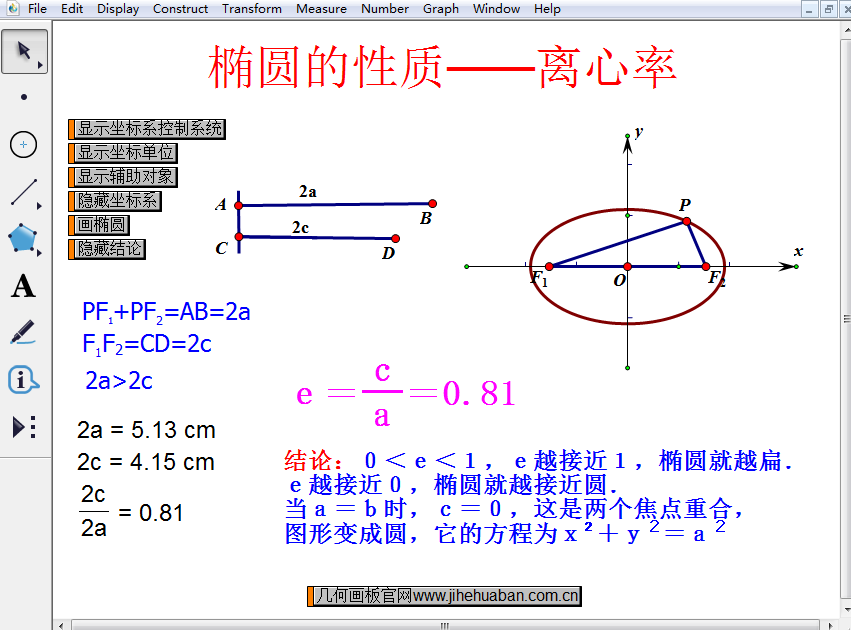
以上课件中，首先是建立了坐标系，然后利用构造轨迹的方法画出了椭圆，并且制作了线段AB、CD来分别控制a和c的值。点击“画椭圆”操作按钮，就可以动态演示过点P构造椭圆的过程。通过演示，就可以得到结论：0＜ｅ＜１，ｅ越接近１，椭圆就越扁． ｅ越接近0，椭圆就越接近圆。

离心率，是一个首先在天文学里使用的名词。一开始人们认为太阳是宇宙的中心，一切星球都是按照圆形轨道绕着太阳运行。后来人们发现这些轨道基本上不是圆，太阳的中心总是偏离轨道的中心，偏离的程度决定了轨道的形状（圆的离心率是0）。于是就用焦点（太阳中心）到轨道中心的距离与半长轴的比来表示轨道的形状，称为离心率。在椭圆里离心率e=c/a就是这样来的。

分析离心率是圆锥曲线的一个重要的几何性质。离心率和曲线形状对照关系综合如下：

到顶点的距离为c、倒定直线的距离为a。

当0＜e=c且a＜1时，轨迹为椭圆；

当e=c且a=1时，轨迹为抛物线；

当e=c且a＞1时，轨迹为双曲线。

点击下面的“下载模板”按钮，即可下载该课件，用来探讨离心率对椭圆形状的影响。通过改变离心率，还可以演示圆锥曲线之间的变换，具体课件可参考：几何画板演示圆锥曲线间的相互转换。