用几何画板比较正多边形和圆的周长

通过学习知道，正多边形就是在圆的基础上得来的，等分圆周就可以得到圆内接正多边形，这个圆就叫做正多边形的外接圆。前面学习了在周长一定的情况下比较多边形和圆的面积，其实在面积一定的条件下，也可以将正多边形和圆的周长进行比较的，从而还可以观察出与圆周长逼近的正多边形的边数。下面就一起学习用几何画板比较正多边形和圆的周长的技巧。

几何画板制作的比较正多边形和圆周长课件样图：

几何画板课件模板——动态演示比较正多边形和圆的周长

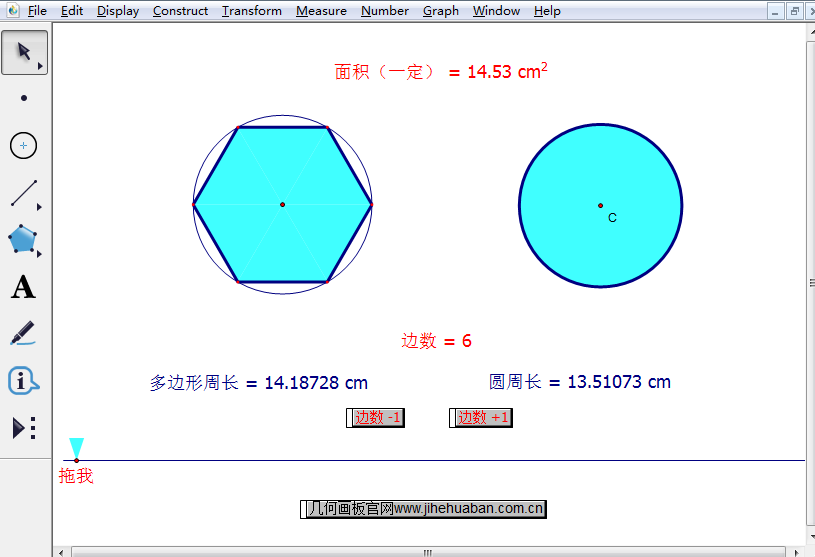
在该课件中，点击“边数-1”操作按钮，就可以将正多边形的边数减一，此时会在多边形下方自动给出该多边形的周长；点击“边数+1”操作按钮，就可以将正多边形的边数加一，此时会在多边形下方自动给出该多边形的周长。也可以手动左右拖动下方直线上的点来改变多边形的边数，只要改变多边形边数，其周长会自动改变。通过不断增加边数，可以发现当多边形边数不断增加时，与圆的周长越逼近。

正多边形与圆的密切联系：

圆既是轴对称图形，又是中心对称图形，且它的每一条直径所在的直线都是它的对称轴，圆具有旋转不变性。

正多边形也是轴对称图形，正n边形有n条对称轴，当n为偶数时，它也是中心对称图形，且绕中心旋转，都能和原来的图形重合。

点击下面的“下载模板”按钮，即可下载该课件，用来给学生们演示面积一定的情况下，正多边形和圆的周长比较，从而找到两者之间的关系。周长一定的情况下，也可以将正多边形和圆的面积进行比较，如有疑问可参考课件：用几何画板比较正多边形和圆的面积。