几何画板演示点的运动路径图像

函数图像形象直观，能清晰地反映现实生活中两个变量之间的函数关系。辨析因运动变化而生成的变量间的函数图像问题，若能对动点运动到图形的特殊点（或“折点”或“拐点”）状态图形给予关注，并借助形成特殊点状态图形的几何性质进行探索，能轻松获解。依托几何图形设置动点或动直线或动图形，因运动而生成两个变量之间的函数关系的图像。在几何画板中，可以借助自定义变换来演示点的运动路径形成的函数图像，下面就一起来学习具体制作技巧。

主动点在路径上的自定义变换课件样图：

几何画板课件模板——演示点的运动路径所形成的函数图像

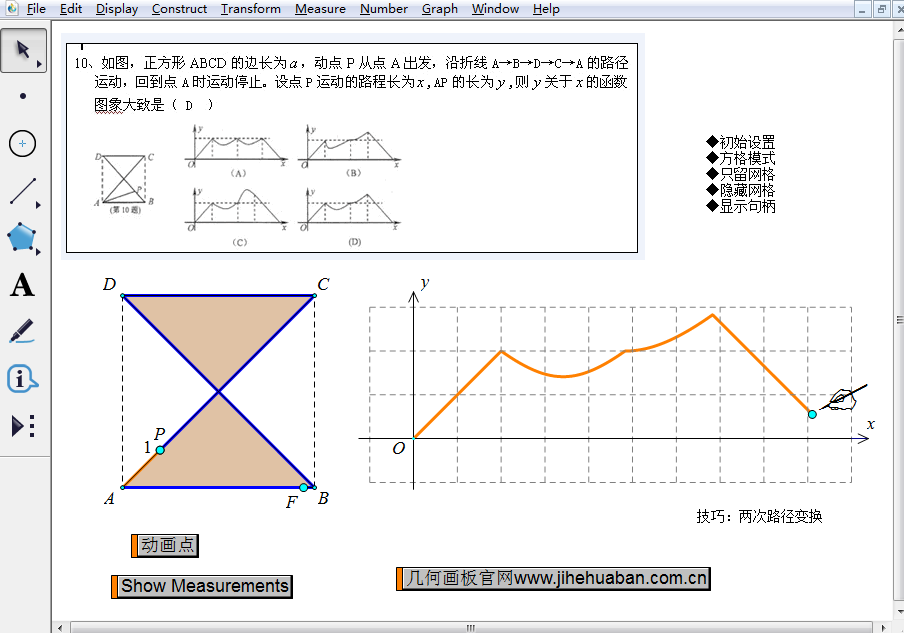
在该课件中，以试卷中常见的一题动点题来讲解的，通过点击“动画点”按钮，从而控制点P沿折线A→B→D→C→A的路径进行运动，从而以点P运动的路程长为自变量，AP的长为因变量，从而求两个变量之间的函数关系。利用自定义变换，从而由点F在AB上运动来控制点P在折线上运动，然后在右边的坐标系中会同时画出点P运动路径的函数图像。

课件中，为了方便观看，将制作过程中用到的一些数据都进行了隐藏，如果想进一步了解制作过程，可以点击“显示度量值”按钮，来查看所有的数据。在课件右上角，是坐标系和网格的控制面板，可以用来对坐标系进行调控。

点击下面的“下载模板”按钮，即可下载该课件，用来演示动点的运动路径所形成的函数图像，从而便于解析这类题目。 这类问题缺少明确的数据信息，常可借助动点运动到特殊点位置时构成的即时状态基本图形的性质并结合图象挖掘隐含信息，利用函数最值及增减性合情推理定性分析。像这类动点求函数图像的题目还有很多，比如可以求面积变化的函数图像，具体课件可参考：几何画板演示点在折线上运动的实例。