几何画板实现三角形和平行四边形互换

三角形和平行四边形是几何图形中比较基础的两个图形，在讲解这两个图形之间的联系时，如果能动态演示给学生们观看三角形是如何转换为平行四边形的，那将有助于学生们理解其中的关系。几何画板作为一款动态几何工具，可以用来演示两者之间的转换动画，下面就一起来学习用几何画板实现三角形和平行四边形互换的技巧。

制作思路：可以先画一个任意三角形，然后以任一边的中点为旋转中心，将三角形旋转180度，这样就得到了平行四边形。

准备工作：下载并安装几何画板软件。点击最新版几何画板免费下载即可获取软件，然后按照提示在电脑上进行安装。

具体制作步骤如下：

步骤一 绘制三角形ABC。打开几何画板软件，选择左侧侧边栏的“多边形工具（不含内部）”，然后在右边的工作区域任意画一个三角形，然后选择文本工具标记三个顶点，记作△ABC。

图1：绘制三角形ABC

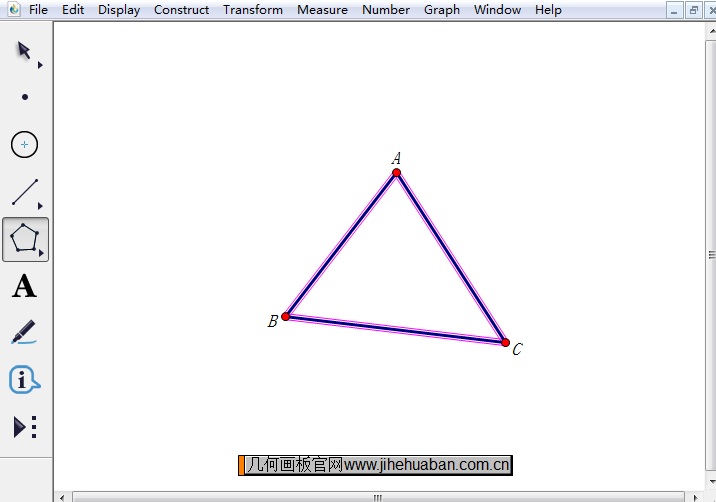
步骤二 构造边AB的中点。鼠标在移动工具状态下选中△ABC的边AB，然后执行“构造”——“中点”命令或按快捷键“Ctrl+M”构造边AB的中点，标记为点D。

图2：构造边AB的中点

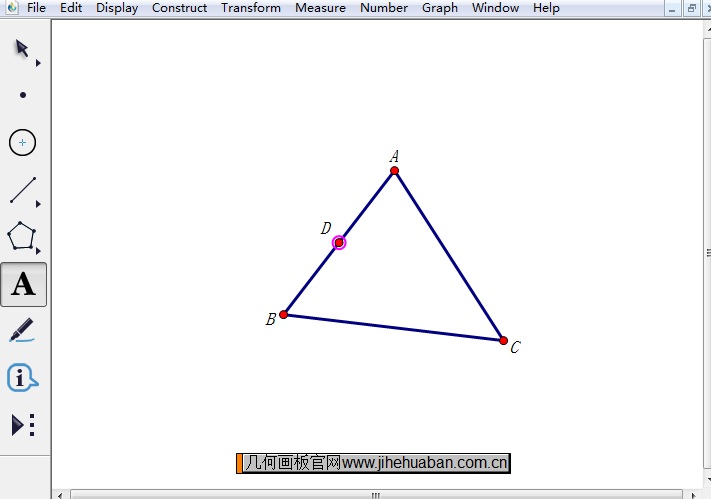
步骤三 标记点D为旋转中心。选中点D执行“变换”——“标记旋转”命令或者直接用鼠标双击点D，将点D标记为旋转中心。

图3：标记点D为旋转中心

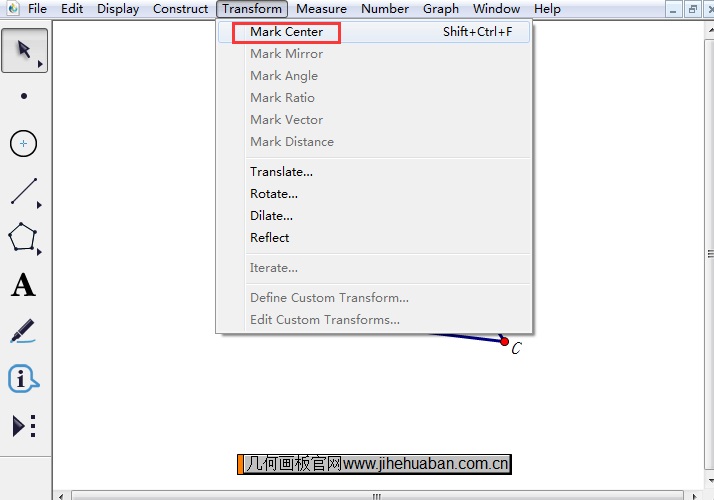
步骤四 新建角度参数t₁。执行“数据”——“新建参数”命令，在弹出的对话框选择角度，单位为度，保留整数数值，然后点击确定。

图4：新建角度参数

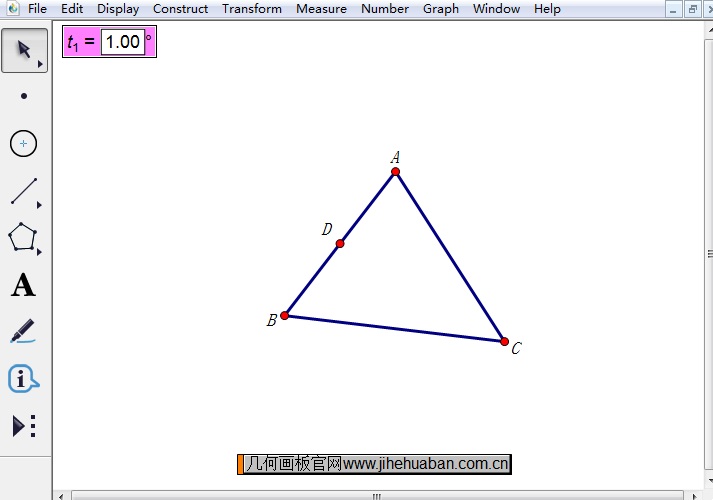
步骤五 选中三角形执行旋转命令。鼠标在选择工具状态下，然后圈选△ABC，执行“变换”——“旋转”命令，在弹出的对话框鼠标单击角度参数，设为按该参数旋转。

图5：选中三角形执行旋转命令

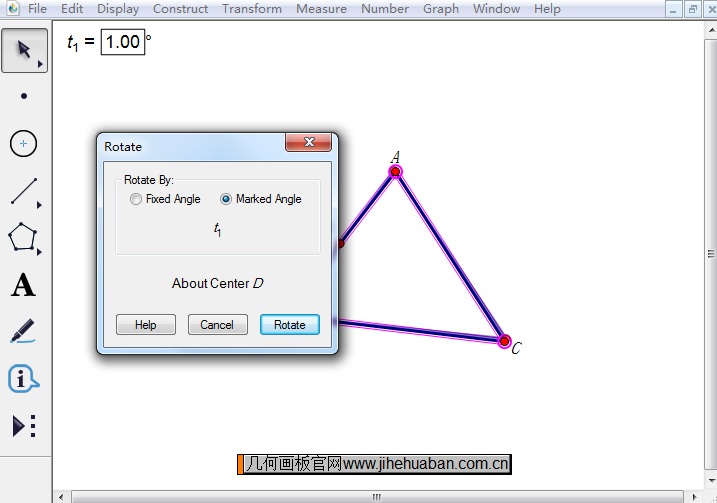
步骤六 改变角度参数的大小，三角形随之转动。选中角度参数，同时按住“Shift键”和“+”，即可使角度参数值增加，从而△ABC也会围绕点D按相应角度旋转。

图6：旋转三角形ABC

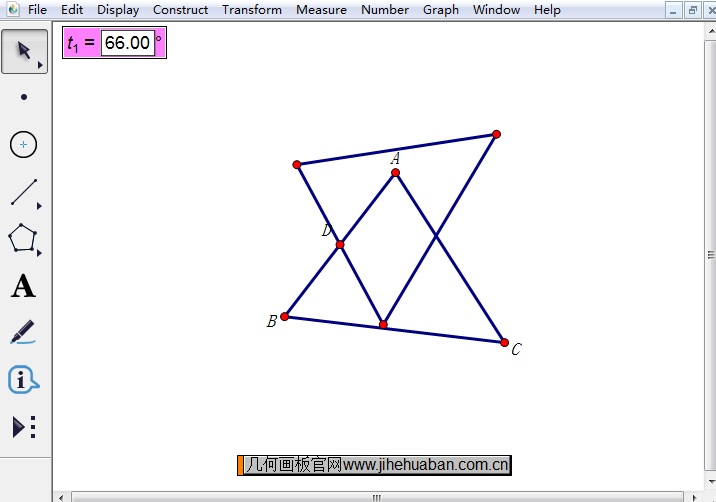
步骤七 当角度参数的值等于180º时，也就是△ABC旋转了180º，此时就出现了平行四边形。

图7：将三角形ABC旋转180度

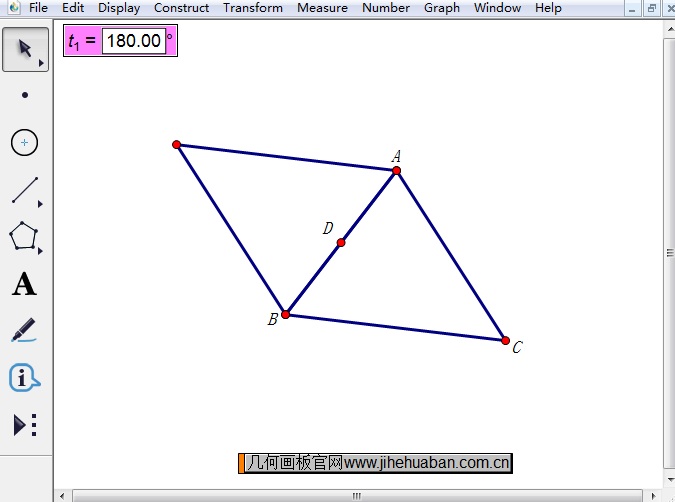
几何画板除了可以用来演示由三角形转换为平行四边形的过程，还可以用来推导平行四边形的面积公式，从而使学生们更加容易理解公式的由来，具体课件可参考：平行四边形的面积公式推导过程演示。

以上就是给大家详细讲解的用几何画板实现三角形和平行四边形互换的具体操作技巧，主要是要确定旋转中心，从而设置旋转角度，然后就可以将三角形进行旋转，从而得到平行四边形了。