根据绘制导函数图像求函数极值

数学中函数的极值不仅在实际问题中占有重要的地位，而且也是函数性态的一个重要特征，下面将通过举例介绍几何画板函数极值和单调区间的求解方法。

具体的操作步骤如下：

1.打开几何画板软件，“绘图”——“绘制新函数”，在函数编辑器中输入下图中的函数解析式，点击“确定”即可。

在函数编辑器输入函数解析式

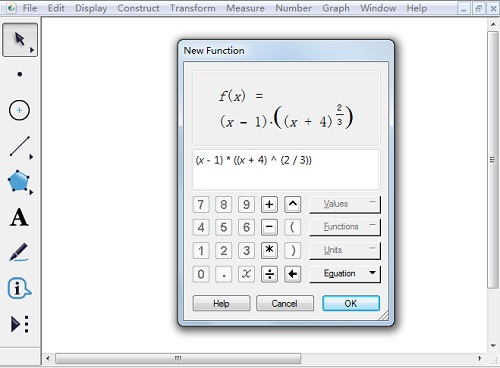
2.右键函数解析式，选择“定义导函数”，出现导函数解析式。右键导函数，选择“绘制函数”，在绘图区域中会出现原函数的导函数（蓝色）。

右键函数定义导函数并绘制导函数图像

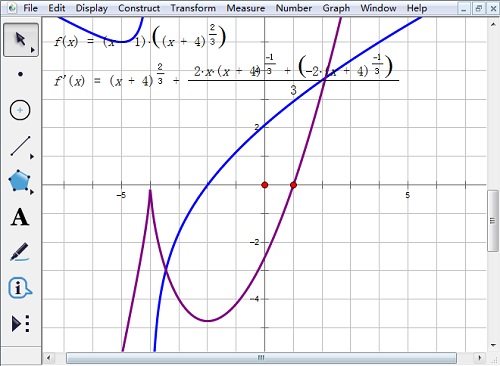
3.选定绘制的导函数图像和x轴，“构造”——“交点”，得到点A。因为原函数在点B处不可导，“绘图”——“绘制点”，绘制点B（-4，0）。

构造导函数与x轴交点且绘制点B

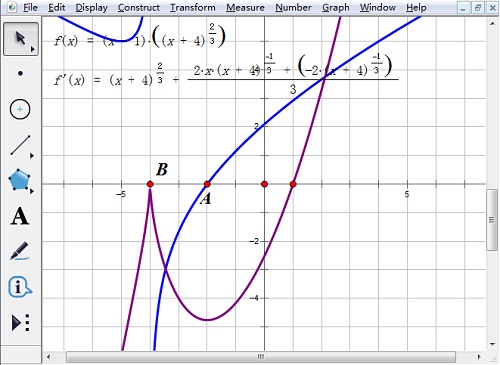
4.选定点B和点A，“度量”——“横坐标”，横坐标值就是原函数单调区间的转折点横坐标。

选定点B和点A执行“度量”——“横坐标”

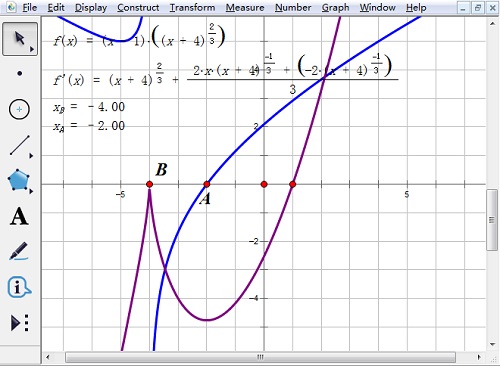
说明：在绘制点B处，导数不存在，故原函数在点B处有极大值0，在点A处有极小值。

以上向大家介绍了几何画板函数极值的求解方法，主要运用了几何画板定义导函数功能，大家多练习几次，就可以熟练掌握了。如需了解关于几何画板函数最值的求解教程，可参考几何画板求函数最值的方法。