教你怎么用几何画板画菲波拉契数列

几何画板在数列中的应用也有很多，不仅可以根据通项公式画出散点图，即使没有通项公式，几何画板也能画散点图，比如菲波拉契数列。下面就介绍用几何画板画菲波拉契数列的方法。

菲波拉契数列：a₁=1，a₂=1，a_n=a_n-1+a_n-2。

1.选择“数据”——“新建参数”f₁=0，f₂=1，选择“数据”——“计算”f₁+f₂，右键选中计算结果，选择“属性”——“标签”改为f₃。继续新建参数a₁=1，计算a₁+1，a₁+1+1，新建参数n=30。

新建参数和图函数并进行相应计算

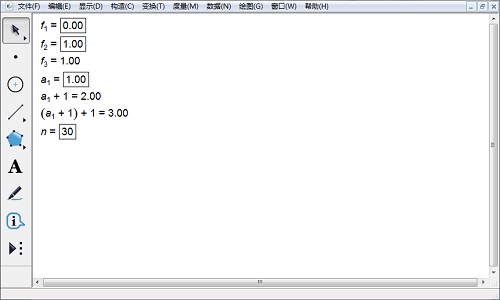
2.依次选择f₁、f₂、a₁、n，按下Shift键，选择“变换”——“深度迭代”。a₁¬——a₁+1，f₁——f₂，f₂——f₃，点击“迭代”。

选中f₁、f₂、a₁、n进行深度迭代

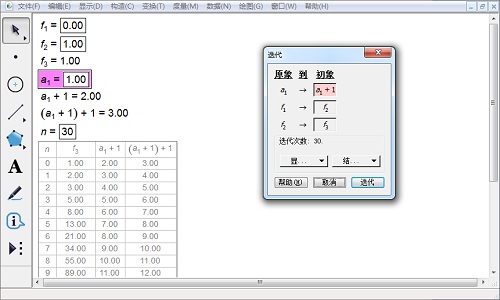
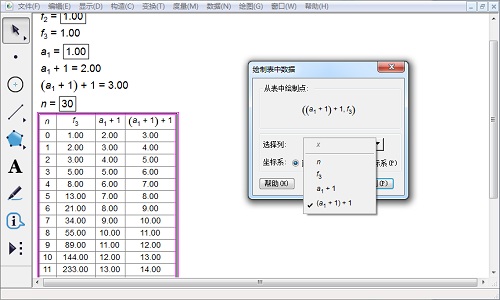
3.右键表格，选择“绘制表中数据”，在弹出的对话框中，在“选择点”一项中点击x，将x列设置为（a₁+1）+1，y列为f₃。

右键迭代数据坂“绘制表中数据”并修改横坐标名称

4.从图象可以看出，数列前面增长得很缓慢，但是到了后面就非常惊人了。

绘制出的散点图示例

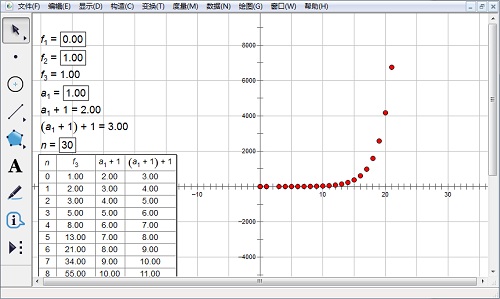
分析：1.数列的前提条件是a₁=1，a₂=1，因为a_n=a_n-1+a_n-2，所以原像是a₁，a₂，初像是a₂，a₃。

2.因为迭代0次的时候f₃=2，所以下标应该是3，而a₁=1，故计算a₁+1+1。

以上内容向大家介绍了几何画板画菲波拉契数列的方法，几何画板数列的应用并不复杂，主要是迭代功能的正确运用。如需了解更多几何画板迭代功能绘制图形的方法，可以参考怎样用几何画板画堆叠正方体正视图。