几何画板怎样求方程的根

一般说来，一元高次方程通常要用图像法求解，我们可以利用几何画板画出方程的图像，那么怎样才能求出方程的根呢？下面将教你使用几何画板求方程的根。

具体的操作步骤如下：

1.以方程x³-3x+1=0为例，先构造函数f(x)= x³-3x+1，画出它的图像。单击“绘图”——“绘制新函数”。在弹出的窗口中输入函数表达式，单击确定。这样函数图象就画好了。

单击“绘图”——“绘制新函数”绘制方程图像

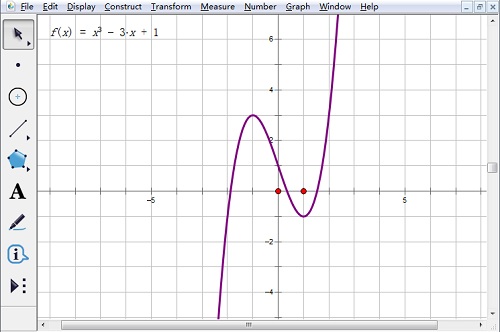
2.选择求根工具。单击“自定义工具”，选择“函数工具”——“f（x）=0的根”这个选项。

在自定义工具下选择函数工具来求方程的根

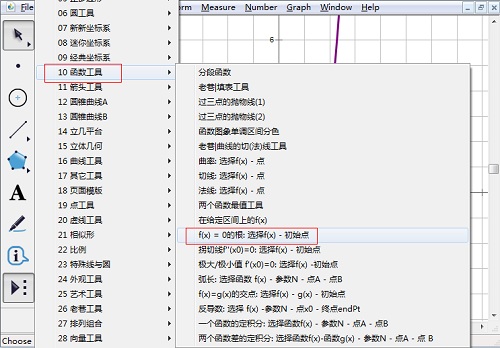
3.单击函数表达式，出现一个活动的点，移动点的位置，直到显示root，这时，显示方程的第一个根，再次点击表达式，移动点得位置，找到第二个根，同样方法可以找到第三个根。

点击函数表达式求出方程的三个根

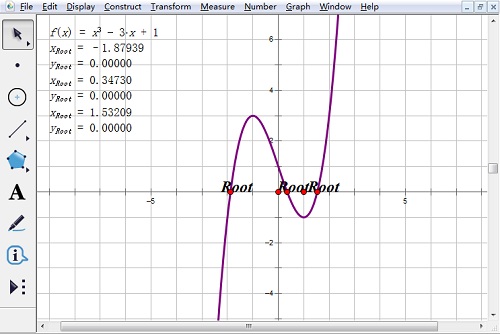
4.更改和设置根的下标。依次单击各x^root值，单击“显示”——“度量值标签”，在小窗口中，下标rod起始值改为1，单击确定。

单击“显示”——“度量值标签”更改根的下标

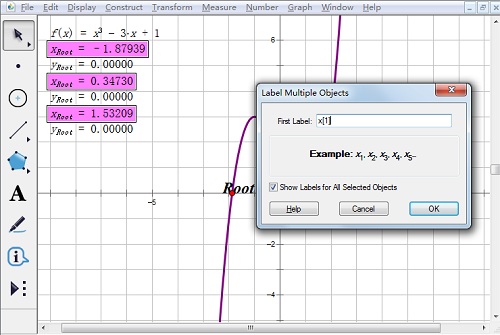
5.隐藏多余的y^root初始值表达式。选择三个初始值，单击“显示”——“隐藏度量值”。

单击“显示”——“隐藏度量值”隐藏多余的初始值

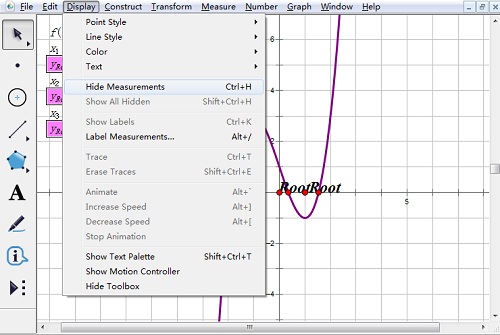
6.设置根的精确度。选中各根，单击“显示”——“度量值的标签”，单击值标签，如果我们要保留两位小数就选择百分之一，确定。

单击“显示”——“度量值的标签”修改根的精确度

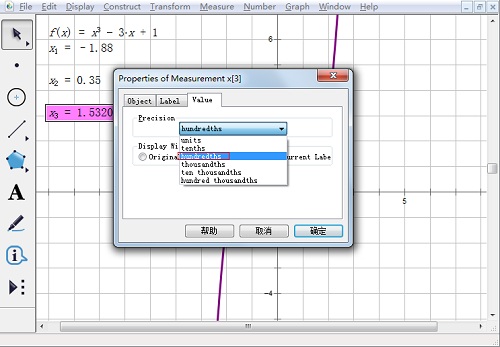
7.最后，显示的结果如下图。

最终方程的根显示结果示例

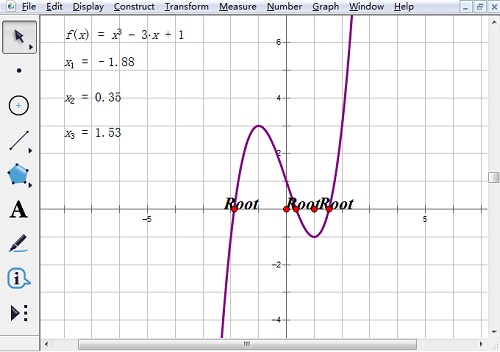
以上给大家讲解了利用几何画板求方程的跟的方法，主要是利用了几何画板自定义工具下的函数工具，使得很便捷地就求出了方程的根。如需了解更多关于几何画板直线方程的教程，可参考几何画板如何求直线的方程。