几何画板演示平行四边形绕中心旋转

作为强大的动态几何工具，几何画板可以让几何图形动起来，实现平移、旋转、折叠等动画效果，然后在课堂上演示给学生们观看，从而可以更容易地明白图形性质，调动课堂积极性。就比如在学习平行四边形时，课本上介绍说该图形能绕着某一点旋转180°后于原来的图形重合，那么平行四边形应该是中心对称图形，下面就一起学习用几何画板制作平行四边形绕中心旋转动画。

几何画板演示平行四边形绕中心旋转课件样图：

几何画板课件模板——演示平行四边形绕中心旋转

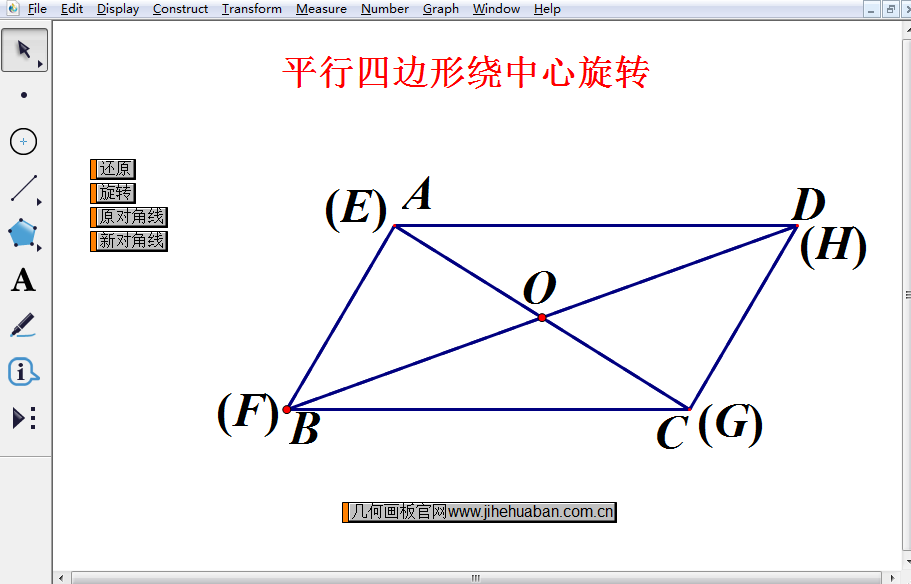
以上课件中，演示的是将平行四边形ABCD绕着中心点O旋转180º，旋转之后与平行四边形EFGH重合，从而可以说明平行四边形是中心对称图形。点击“旋转”按钮，就可以自动演示将将平行四边形ABCD绕着中心点O旋转180º，然后就会发现与平行四边形EFGH重合。如果要显示原图形的对角线就点击“原对角线”按钮，就可以显示原图形的对角线；点击“新对角线”按钮，就可以显示当前图形的对角线。一个是实线，一个是虚线，这样就便于认识。

通过演示该课件，我们知道：

平行四边形是中心对称图形，绕对角线的交点旋转180度能与原图形重合。而两条对角线的交点就是它的对称中心。

1.如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。

2.如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等。

3. 如果一个四边形是平行四边形，那么这个四边形的邻角互补。

4. 如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分。

点击下面的“下载模板”按钮，即可下载该课件，用来给学生们演示平行四边形绕中心旋转，让学生们直观感受平行四边形的中心对称性质，从而加深对该图形的认识。另外几何画板作为教学辅助工具，可以用它来推导平行四边形面积公式，如果有疑问，可参考课件：平行四边形的面积公式推导过程演示。