几何画板演示多边形内角和

三角形是最简单的一种多边形，我们平常接触较多的多边形就是三角形和四边形，还有一些五边形和六边形也比较常见。对于多边形，我们经常会需要研究它的内角和和外角和。三角形和四边形的内角和我们很熟悉，分别是180度和360度，那五边形、六边形的内角和呢？n边形的内角和呢？下面就来介绍几何画板多边形内角和的推理。

几何画板演示多边形内角和课件样图：

几何画板演示《多边形内角和》课件示例

对于多边形的内角和，我们一个一个度量再相加是不现实的，三角形四边形可以，五边形六边形勉强也可以，但是度量的方法还有误存在，当n边形的边数很多时，手动测量的方法并不可行，因此如果我们能够寻找出n边形计算内角的一些规律性的东西，那么对于我们计算分析是非常有帮助的。

观察多边形并进行推理计算

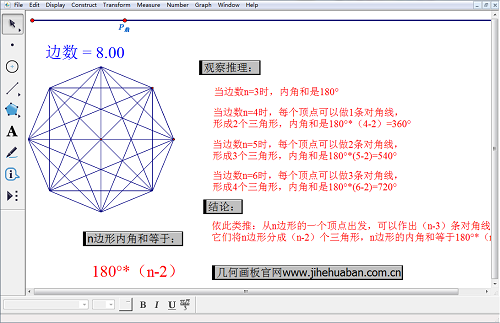
拖动最上方横线上的P点，会发现多边形的边数在不断地改变，图形也在相应的变化，图形中也相应显示出了对角线的情况。点击右边“观察推理”按钮，我们可以知道：

当边数n=3时，内角和是180°；

当边数n=4时，每个顶点可以做1条对角线，形成2个三角形，内角和是180°*（4-2）=360°；

当边数n=5时，每个顶点可以做2条对角线，形成3个三角形，内角和是180°*(5-2)=540°；

依此类推：从n边形的一个顶点出发，可以作出（n-3）条对角线，它们将n边形分成（n-2）个三角形，n边形的内角和等于180°*（n-2）。

最后总结出n边形的内角和公式计算公式是：180°*（n-2）

点击下面的“下载模板”就可以将课件下载下来进行演示了。多边形的内角和是一个比较重要知识点，学生必须要理解清楚这一点才能够进行相关的计算与分析，不仅几何画板内角和可以演示推理出来，几何画板多边形外角和也可以演示。具体可以参考教程：几何画板动态演示多边形的外角和。