利用几何画板动态演示阿波罗尼斯圆

阿氏圆又称阿波罗尼斯圆，已知平面上两点A、B，则所有满足PA/PB=k且不等于1的点P的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆。几何画板作为研究几何定理的辅助工具，可以用它来探究阿波罗尼斯圆，下面就一起学习用几何画板制作阿氏圆课件的方法。

几何画板动态演示阿波罗尼斯圆课件样图：

几何画板课件模板——动态演示阿波罗尼斯圆示例

在该课件中，已经度量出了线段PA、PB的长度，并且计算了PA/PB的值。通过用移动工具选中圆上的动点P并在圆上进行拖动，此时线段PA、PB的长度的长度也是一直在变化的，但是唯一恒定不变的就是PA/PB的比值，则验证了点P经过的轨迹所组成的圆就是阿波罗尼斯圆。

基本性质如下：

由阿波罗尼斯圆可得阿波罗尼斯定理，即：

设三角形的三边和三中线分别为a、b、c、m1、m2、m3，则有以下关系：

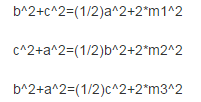
（此定理用余弦定理和勾股定理可以证明）。

通过学习该课件，可以得知：

1.到两定点的距离之商为定值的点的轨迹是阿波罗尼斯圆。

2.到两定点的距离之和为定值(比这两点之间的距离要大)的点的轨迹是椭圆。

3.到两定点的距离之差为定值(比这两点之间的距离要小)的点的轨迹是双曲线。

4.到两定点的距离之积为定值的点的轨迹是卡西尼卵形线。

阿波罗尼斯圆这个概念在课本中并未明确给出，但是最近几年的高考题目中往往出现此类题目，所以说掌握好这个几何定理，也是很有必要的。简单来说就是到两定点的距离之商为定值的点的轨迹是阿波罗尼斯圆，点击下面的“下载模板”按钮，即可下载该课件，用来给学生们动态演示阿波罗尼斯圆，方便学生全面理解该知识。利用几何画板可以验证绝大多数几何学中的定理，比如托勒密定理，具体可参考：利用几何画板验证托勒密定理。